模型量化
量化简介
模型量化
模型量化是指在保持推理精度损失较低的情况下,将连续取值如
常用的数据类型
- FP32: 32位浮点数,是最常用的高精度表示方式。
- FP16: 16位浮点数,数值范围比
小,但占用内存较少。 - BF16: 16位截断的
,增加指数位,数值范围更广,常用于深度学习。 - INT8: 8位整数,位数仅为
的1/4,适用于模型参数的数据范围映射。 - INT4: 4位整数,进一步减少位数,适用于极端资源受限的场景。
- 二值网络(Binary Network): 1位二值网络,参数只能取0或1,计算效率极高但精度损失较大。
工业界目前最常用的量化位数是8比特,低于8比特的量化被称为低比特量化。1比特是模型压缩的极限,可以将模型压缩为1/32,在推理时也可以使用高效的
量化对象
- 权重(Weight):权重的量化是最常规的,可达到减少模型大小内存和占用空间。
- 激活值(Activation): 实际中激活值往往是占内存使用的大头,量化激活值不仅可以大大减少内存占用,更重要的是,结合权重的量化可以充分利用整数计算获得性能提升。
- KV Cache: 量化 KV 缓存对于提高长序列生成的吞吐量至关重要。
- 梯度(Gradients): 相对上面的量化对象略微小众一些,因为主要用于训练。在训练深度学习模型时,梯度通常是浮点数,它主要作用是在分布式计算中减少通信开销,也可以减少反向传播时的开销。
量化形式
根据量化数据表示的原始数据范围是否均匀,可以将量化方法分为线性量化和非线性量化
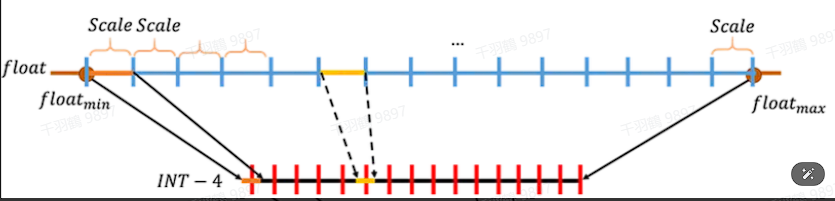
深度神经网络的权重和激活值通常是不均匀的,因此理论上使用非线性量化导致的精度损失更小,但在实际推理中非线性量化的计算复杂度较高,通常使用线性量化:
其中

根据
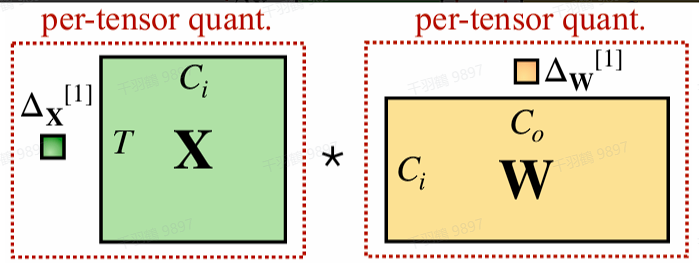
逐层量化 per-tensor
范围最大,最简单,以一层网络为单位一组量化参数。
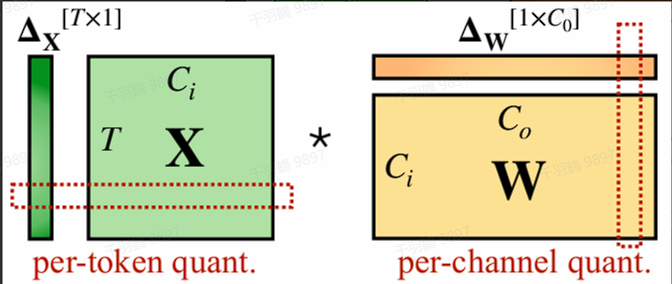
逐通道量化 per-token & per-channel
以一层网络的每个量化通道为单位,每个通道单独用一组量化参数。量化粒度更细,更高的量化精度,计算也更复杂。其中,per-token 针对激活
逐组量化 per-group
以组为单位,每个组比如
此外激活值和权重可以选择不同的粒度进行量化,对于激活值来说还有动态量化(推理过程中,实时计算激活的量化系数,对激活进行量化)与静态量化(在推理前就计算好激活的量化系数,在推理过程中应用)。
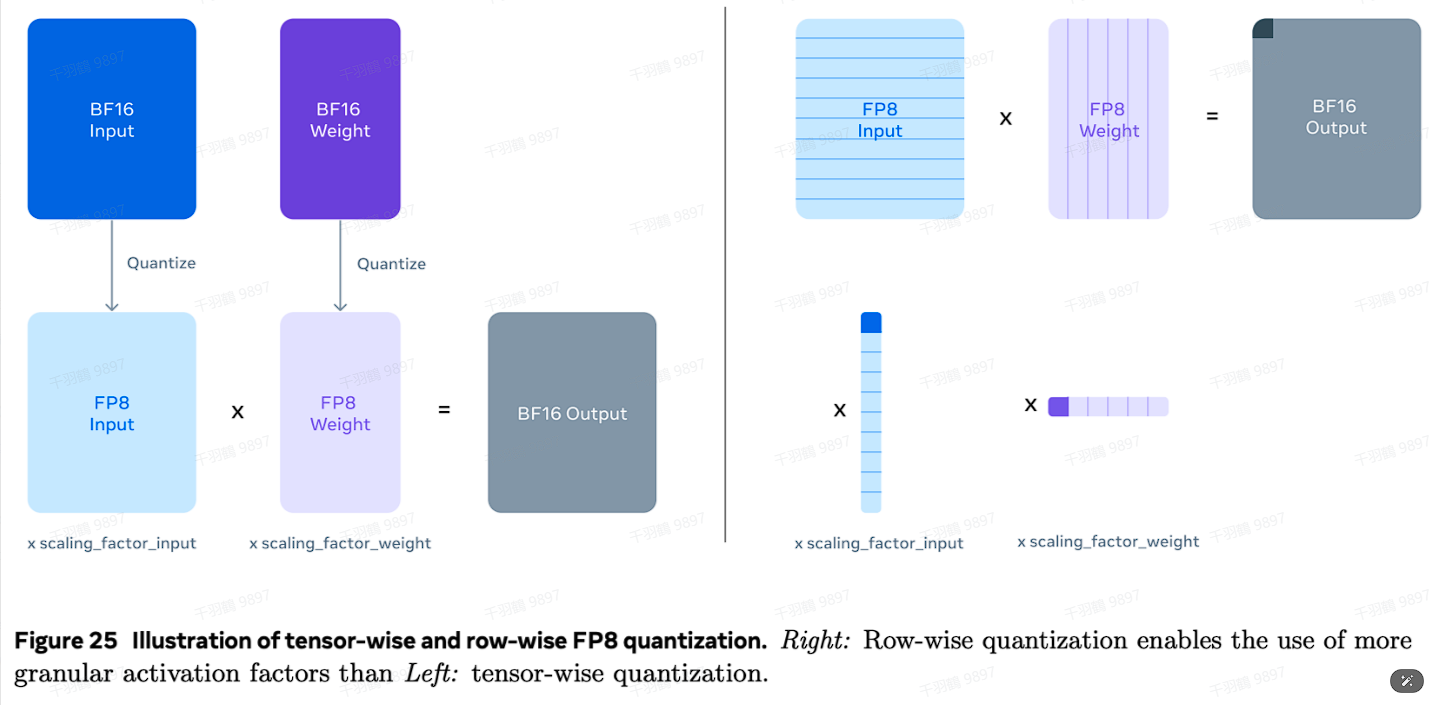
Llama3 技术报告中提供的 tensor-wise 和 row-wise FP8 量化示意图
在 Llama3 技术报告中,提供了 tensor-wise 和 row-wise 的 FP8 量化示意图,这些示意图展示了不同粒度下的浮点数到整数的转换过程,帮助理解不同粒度选择对于模型性能和计算复杂度的影响。
量化分类
在深度学习模型的部署中,模型的大小和推理速度是两个非常重要的因素。为了在不显著损失模型准确率的前提下减小模型大小并加快推理速度,量化技术应运而生。量化技术通过将模型参数和计算从浮点数表示转换为低精度表示(如 8 位整数)来实现这一目标。根据量化压缩模型的阶段,量化可以分为以下几类:
量化感知训练 Quantization Aware Training (QAT)
量化感知训练(QAT)是在模型训练过程中引入量化的意识。具体来说,在训练过程中,尽管模型的权重和激活值仍然以浮点数形式存储和更新,但在前向传播时会模拟低精度运算。这种方法使得模型在训练过程中就能够适应量化带来的噪声,从而在部署时能够更好地保持性能。
QAT 的主要优势在于其能够在保持模型准确率的同时实现显著的压缩效果。然而,由于需要在训练过程中进行额外的模拟计算,QAT 的训练时间可能会有所增加。
量化感知微调 Quantization-Aware Fine-tuning (QAF)
量化感知微调(QAF)是一种在已有的预训练模型基础上进行微调的量化方法。与 QAT 类似,QAF 在微调过程中也会引入量化的意识。然而,由于其基于预训练模型进行微调,因此训练时间通常较短。
QAF 的优势在于其能够在较短的时间内获得接近 QAT 的量化效果,是一种兼顾效率与性能的方法。
训练后量化 Post Training Quantization (PTQ)
训练后量化(PTQ)是指在模型训练完成后,对其进行量化处理的一种方法。PTQ 不需要在训练过程中考虑量化问题,因此可以直接应用于任何已经训练好的模型。
虽然 PTQ 的实施非常简单,并且不会增加训练时间,但其效果通常不如 QAT 和 QAF,因为模型在训练过程中没有机会适应量化引入的噪声。然而,对于一些特定的应用场景,PTQ 仍然是一个快速而有效的选择。
QAT 量化感知训练
在深度学习模型的训练和部署过程中,模型的精度和计算效率往往是两个重要的考量因素。为了在这两者之间取得平衡,量化感知训练(Quantization Aware Training, QAT)成为了一种有效的方法。本文将介绍QAT的基本原理及其在大语言模型(LLM)中的具体应用。
量化感知训练的基本原理
量化感知训练首先需要对模型进行正常的预训练。在此基础上,模型中会插入“伪量化节点”,即对权重和激活进行量化和反量化操作。这种方法的目的在于引入量化误差,使得模型在训练过程中能够“感知”到量化操作,从而在优化训练误差的同时兼顾量化误差。这种方法特别适用于对模型精度要求较高的场景,其量化目标无缝地集成到模型的训练过程中,使得大语言模型(LLM)在训练过程中能适应低精度表示,增强其处理由量化引起的精度损失的能力。
QAT方法
LLM-QAT
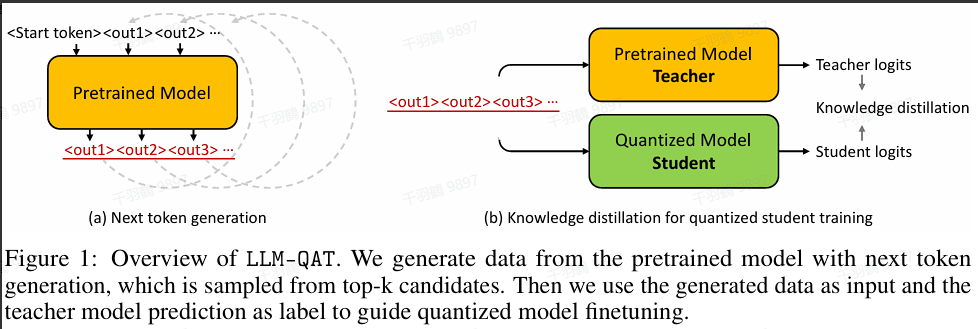
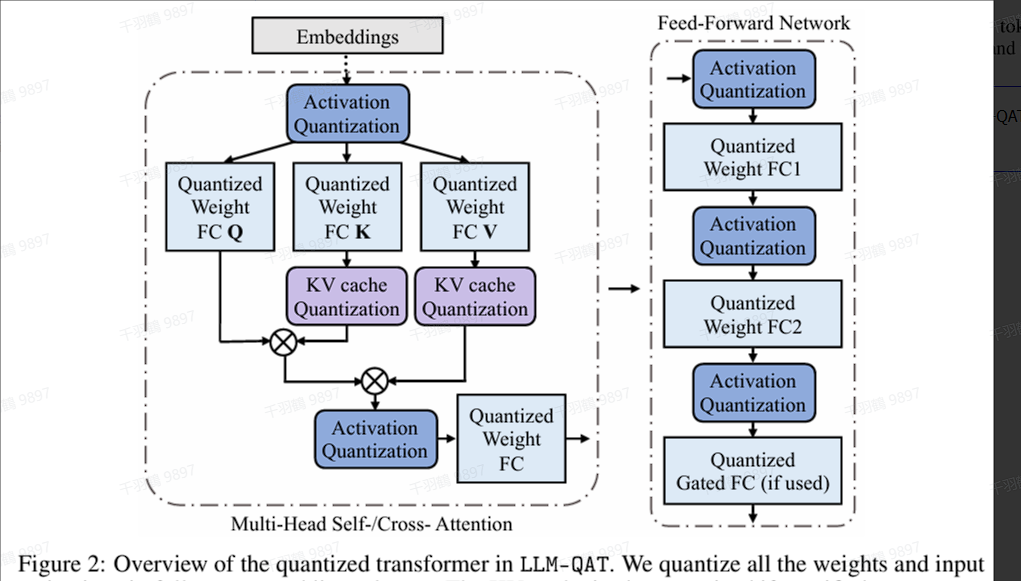
LLM-QAT是一种利用预训练模型生成结果来实现无数据蒸馏的方法。通过这种方法,我们不仅可以量化模型的权重和激活,还可以量化KV缓存。这样的策略旨在增强吞吐量并支持更长的序列。这意味着,LLM-QAT能够将带有权重和KV缓存量化的LLaMA模型蒸馏为仅有4比特的模型。
这种方法不仅提高了计算效率,还在一定程度上保留了模型精度,使得在资源受限的环境中部署大规模语言模型成为可能。
QAF 量化感知微调
在微调过程中对大型语言模型(LLM)进行量化的主要目标是确保经过微调的LLM在量化为较低位宽后仍保持性能。通过将量化感知整合到微调中,可以在模型压缩和保持性能之间取得平衡。
QAF方法
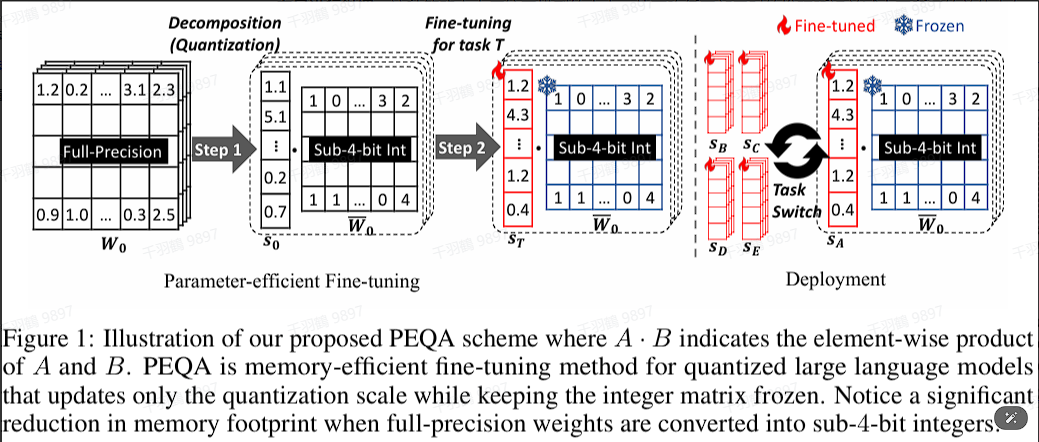
PEQA:Memory-Efficient Fine-Tuning of Compressed Large Language Models via sub-4-bit Integer Quantization
PEQA是一种新的量化感知微调技术,可以促进模型压缩并加速推理。它采用了双阶段过程运行:
- 第一阶段:每个全连接层的参数矩阵被量化为低比特整数矩阵和标量向量。
- 第二阶段:对每个特定下游任务的标量向量进行微调。
这种策略大大压缩了模型的大小,从而降低了部署时的推理延迟并减少了所需的总体内存。同时,使快速的微调和高效的任务切换成为可能。
QLoRA
QLoRA也是一种QAF方法,具体内容可以参考3.5.6章节。
PEFT 参数高效微调
在参数高效微调(PEFT)中,目标是通过最小化参数调整来实现最大化的模型性能改进。这种方法不仅节省计算资源,还能在多任务环境中灵活应用。QLoRA作为QAF方法的一种实现,体现了PEFT的理念。
PTQ 训练后量化
在深度学习领域,特别是大规模语言模型(LLM)的应用中,模型的存储和计算成本一直是一个重要的挑战。为了应对这一挑战,量化技术被广泛应用于减少模型的复杂性和提高效率。本文将探讨几种常用的训练后量化(PTQ)方法。
QAT 插入“伪量化节点”后微调
量化感知训练(QAT)通过在训练过程中插入“伪量化节点”来模拟量化效果,以便在推理阶段更好地适应量化后的模型。然而,这种方法大大增加了计算成本,尤其是在面对超大规模的 LLM 时。目前,针对 LLM 的量化研究主要集中在训练后量化(PTQ),例如 LLM.int8()、SmoothQuant 和 GPT-Q。对于权重而言,可以在推理前事先计算好量化系数,完成量化。但是对于激活值(即各层的输入),它们事先是未知的,取决于具体的推理输入。
训练后量化(PTQ)
在LLM训练完成后对其参数进行量化,只需要少量校准数据,适用于追求高易用性和缺乏训练资源的场景。主要目标是减少LLM的存储和计算复杂性,而无需对LLM架构进行修改或进行重新训练。PTQ的主要优势在于其简单性和高效性,但PTQ可能会在量化过程中引入一定程度的精度损失。
PTQ方法
LLM.int8()
在激活值
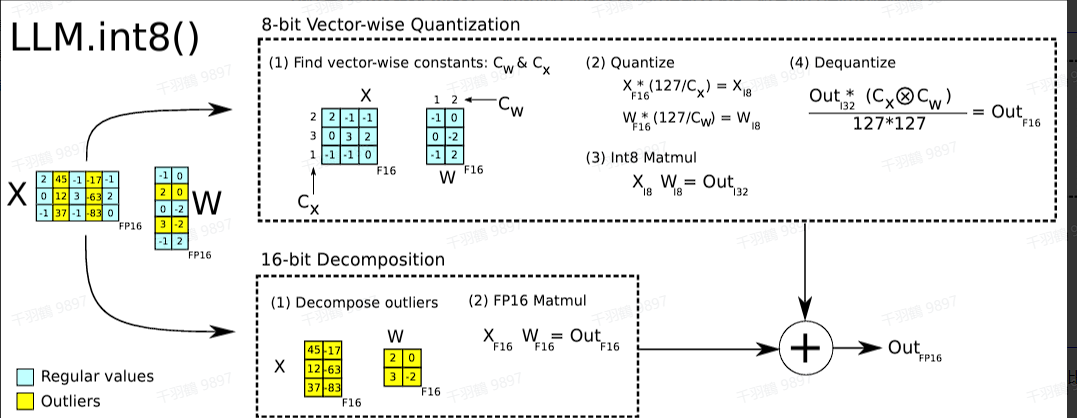
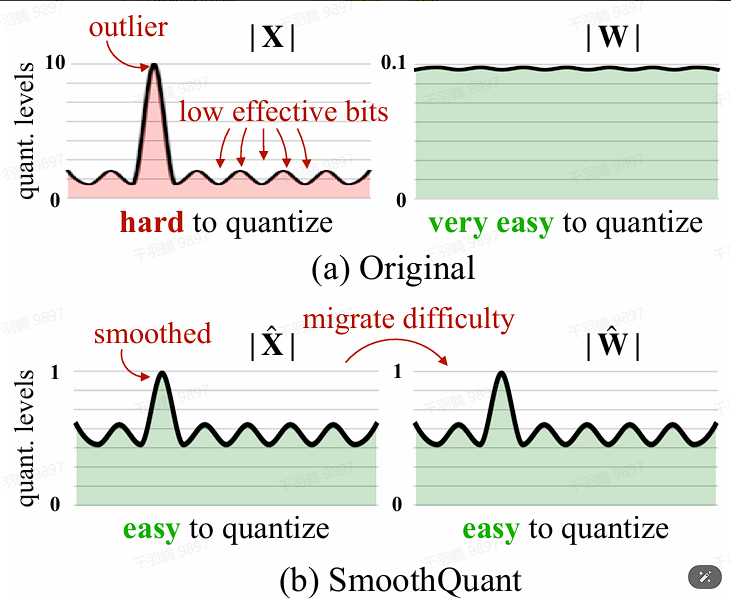
SmoothQuant
针对激活中的离群值,SmoothQuant 给出了与 LLM.int8() 不同的解题思路。激活值的量化比权重的量化难得多,可以通过一个平滑系数,把二者的难度中和一下:
其中,平滑系数
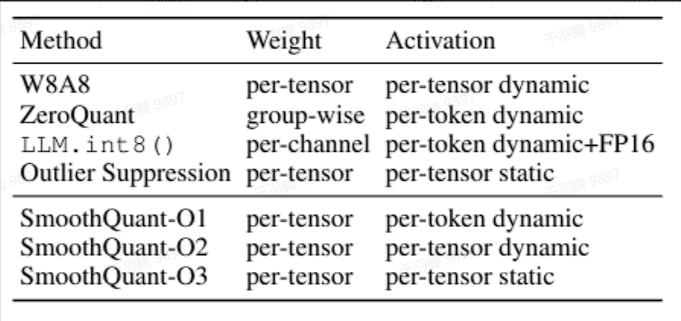
对平滑后的激活值和权重进行量化即可。权重采用 per-tensor 方式,激活采用不同粒度、不同时机的量化有不同版本。
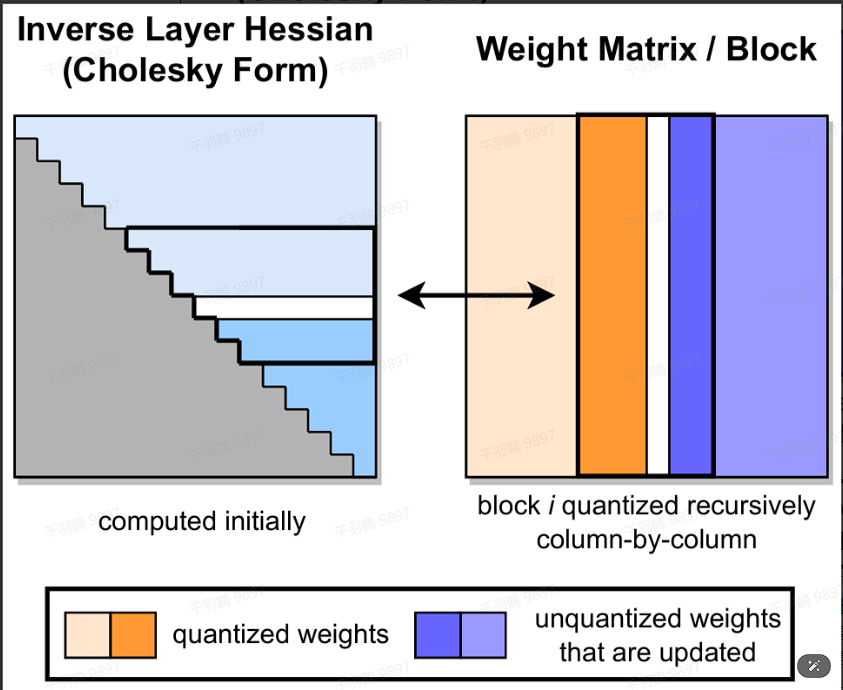
GPT-Q
LLM.int8() 和 SmoothQuant 都属于 round-to-nearest (RTN) 量化:舍入到最近的定点数。GPT-Q 则是把量化问题视作优化问题,逐层寻找最优的量化权重。对某个块(block)内的所有参数逐个量化,每个参数量化后,需要适当调整这个块内其他未量化的参数,以弥补量化造成的精度损失。此外,GPTQ 量化需要准备校准数据集。
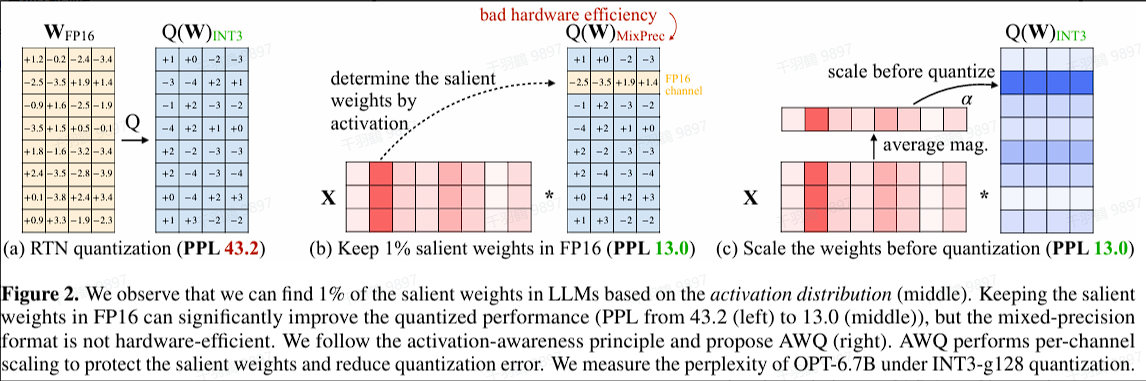
AWQ: 对于LLM的性能, 权重并不是同等重要的,通过保留$$1%$$的显著权重可以大大减少量化误差。在此基础上,AWQ采用了激活感知方法,考虑与较大激活幅度对应的权重通道的重要性,这在处理重要特征时起着关键作用。采用逐通道缩放技术来确定最佳缩放因子,从而在量化所有权重的同时最小化量化误差。