FlashAttention Forword流程

FlashAttention Forward流程

在这篇博客文章中，我们将深入探讨FlashAttention的前向流程，尤其是其独特的分块计算方法。FlashAttention通过引入额外的统计量，解决了注意力计算中Softmax分块计算的难题，并通过kernel融合优化了计算效率。

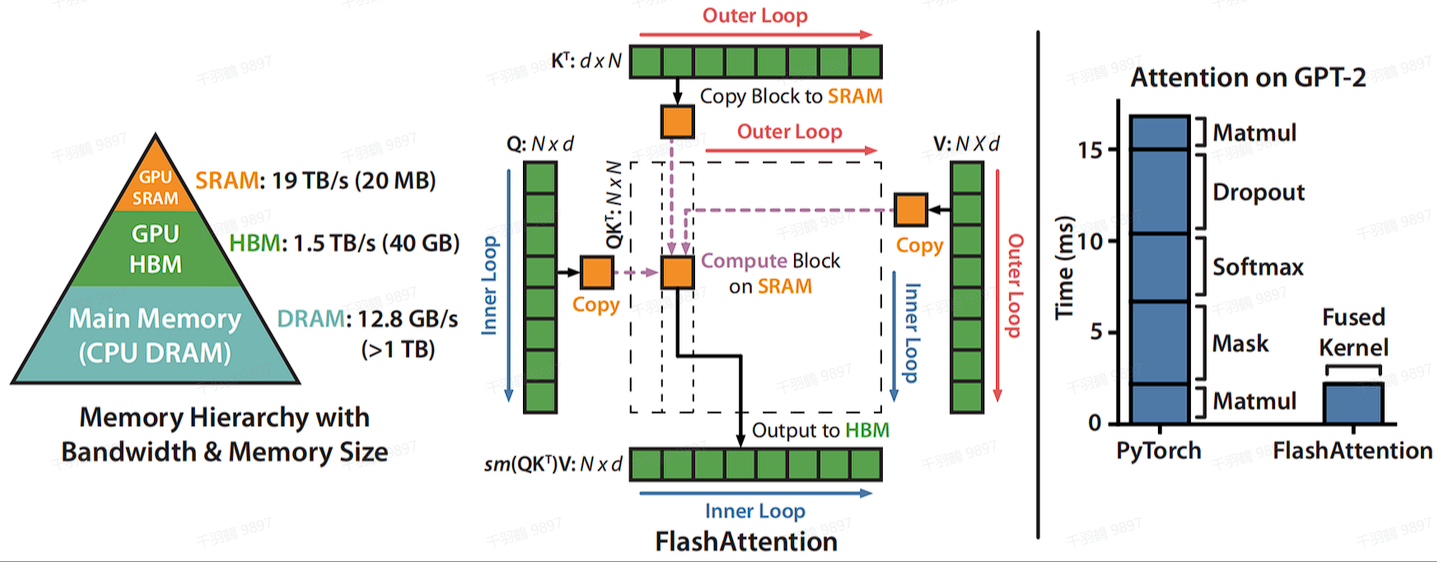
Tiling 分块计算

SRAM的读写速度比HBM高一个数量级，但内存小很多。通过kernel融合的方式，将多个操作融合为一个操作，利用高速的SRAM进行计算，可以减少读写HBM的次数，从而有效减少内存受限操作的运行时间。但SRAM的内存大小有限，不可能一次性计算完整的注意力，因此必须进行分块计算，使得分块计算需要的内存不超过SRAM的大小。

分块计算的难点

注意力计算流程是矩阵乘法 $\to$ scale $\to$ mask $\to$ softmax $\to$ dropout $\to$ 矩阵乘法。矩阵乘法和逐点操作的分块计算是容易实现的，但是Softmax由于分母需要完整输入数据，所以分块计算很难。

FlashAttention的做法

引入额外的统计量

为了实现Softmax分块计算，FlashAttention引入了额外的统计量 $m (x)$ 和 $l (x)$ 来进行解耦。通过这些统计量，可以求得Safe Softmax，并解耦拼接向量的Softmax计算。

公式说明

$m (x) = m ([x^{(1)}, x^{(2)}]) = max (m (x^{(1)}), m (x^{(2)}))$
$f (x) = [e^{m (x^{(1)}) - m (x)} f (x^{(1)}), e^{m (x^{(2)}) - m (x)} f (x^{(2)})]$
$l (x) = l ([x^{(1)}, x^{(2)}]) = e^{m (x^{(1)}) - m (x)} l (x^{(1)}) + e^{m (x^{(2)}) - m (x)} l (x^{(2)})$
$softmax (x) = \frac{l (x)}{f (x)}$

通过保持额外的两个统计量可以实现Softmax的分块计算，同时注意，多个block的Softmax，GPU是可以做并行计算的，这也提升了计算效率。

Kernel融合

在FlashAttention中，通过kernel融合，将mask和dropout加上的forward过程整合为一个操作：

$S = \frac{1}{\sqrt{d_{k}}} Q K^{T} \in R^{N \times N}$
$S_{masked} = MASK (S) \in R^{N \times N}$
$P = softmax (S_{masked}) \in R^{N \times N}$
$P_{dropped} = dropout (P, p_{drop}) \in R^{N \times N}$
$O = P_{dropped} V \in R^{N \times d}$

Tiling分块计算使得可以用一个CUDA kernel来执行注意力的所有操作，从HBM中加载输入数据，在SRAM中执行所有的计算操作（矩阵乘法，mask，softmax，dropout，矩阵乘法），再将计算结果写回到HBM中，通过kernel融合将多个操作融合为一个操作，避免了反复地从HBM中读写数据。

一个分块计算Softmax的例子

为了更好地理解分块计算Softmax，我们来看一个简单的例子：对向量 $[1, 2, 3, 4]$ 计算Softmax，分成两块 $[1, 2]$ 和 $[3, 4]$ 进行计算。

计算block1：

$m_{1} = max ({1, 2}) = 2$
$f_{1} = [e^{1 - 2}, e^{2 - 2}] = [e^{- 1}, e^{0}]$
$l_{1} = \sum f_{1} = e^{- 1} + e^{0}$
$o_{1} = l_{1} f_{1} = (e^{- 1} + e^{0}) [e^{- 1}, e^{0}]$

计算block2：

类似的方法可以用于计算第二个block。

通过这些步骤，我们可以有效地进行分块计算Softmax，从而提升计算效率。

Forward具体流程

Flash Attention 具体做法

首先，将 $Q$ 矩阵切为 $T_{r}$ 块（block），每块的长度为 $B_{r}$ 。用 $Q_{i}$ 来表示切完后的某块矩阵，则 $Q_{i}$ 的维度为 $(B_{r}, d)$ 。不难理解， $Q_{i}$ 中存储着某 $B_{r}$ 个 token 的 query 信息。

然后，将 $K^{T}$ 矩阵切为 $T_{c}$ 块，每块的长度为 $B_{c}$ 。用 $K_{j}^{T}$ 表示切完后的某块矩阵，则 $K_{j}^{T}$ 的维度为 $(d, B_{c})$ 。易知 $K_{j}^{T}$ 中存储着某 $B_{c}$ 个 token 的 key 信息。

同样，将 $V$ 矩阵也切为 $T_{c}$ 块，每块长度为 $B_{c}$ 。用 $V_{j}$ 表示切完后的某块矩阵，则 $V_{j}$ 的维度为 $(B_{c}, d)$ 。易知 $V_{j}$ 中存储着某 $B_{c}$ 个 token 的 value 信息。

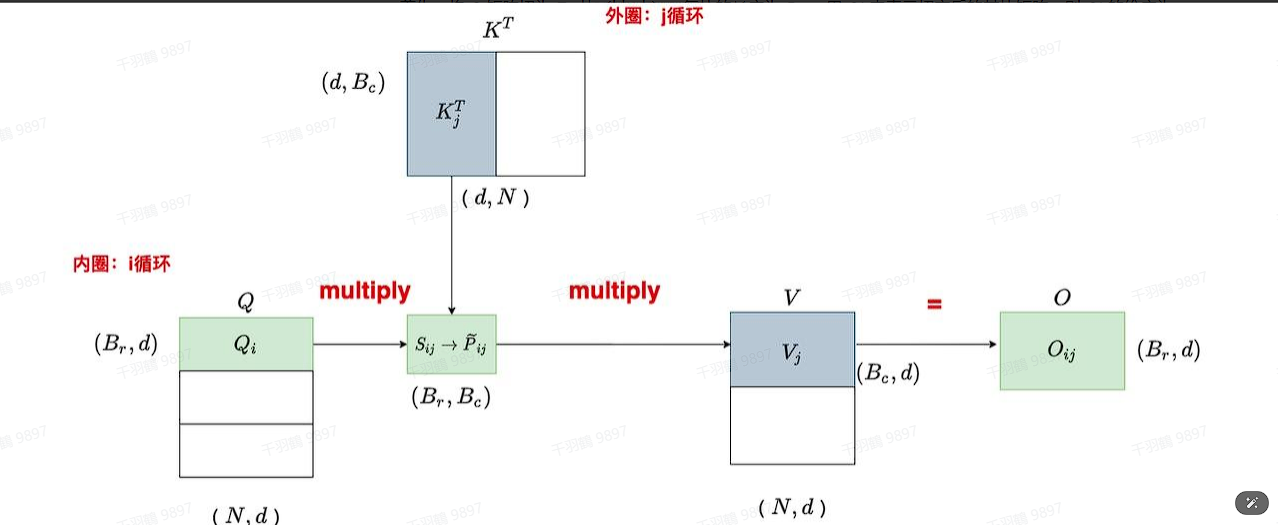
计算初始attention分数

图中的 $S_{i j}$ 表示前 $B_{r}$ 个token和前 $B_{c}$ 个token间的原始相关性分数。

afe softmax + mask + dropout

对 $S_{i j}$ 做safe softmax、mask和dropout操作，得到 $P_{i j}$ 。你可能会有疑惑：前面不是说， $P_{i j}$ 是归一化前的结果， $P_{i j}$ 是归一化后的结果吗？那么这里是不是应该用 $P_{i j}$ 呢？这里确实只用到算到 $P_{i j}$ ，在后文对分块计算细节的讲解中，我们会详细说这点。目前为止，大家不用太纠结符号，只用大体知道 $P$ 代表的含义即可。

计算output

细心的你肯定又发现了，这个等式不太对劲，这个 $O_{i j}$ 不太对劲。想一想，在正常情况下，前 $B_{r}$ 个token过attention后的输出结果，应该是它和所有token都做注意力计算后的输出结果。可是这里， $O_{i j}$ 却只是前 $B_{r}$ 个token和前 $B_{c}$ 个token的结果。虽然 $O_{i j}$ 的shape对了，但其中的内容却不是我们最终想要的。所以，关于 $O$ 的计算，也是我们需要关注的细节，我们同样放在后文详说。

计算的伪代码

# 代码块
# ---------------------
# Tc: K和V的分块数
# Tr: Q的分块数量
# ---------------------

for 1 <= j <= Tc:

    for 1 <= i <= Tr:

        do....

图例加深理解

下面给出具体的图例加深理解（假设 $T_{r}$ 等于 2， $T_{c}$ 也等于 2）:

当 j=1 时

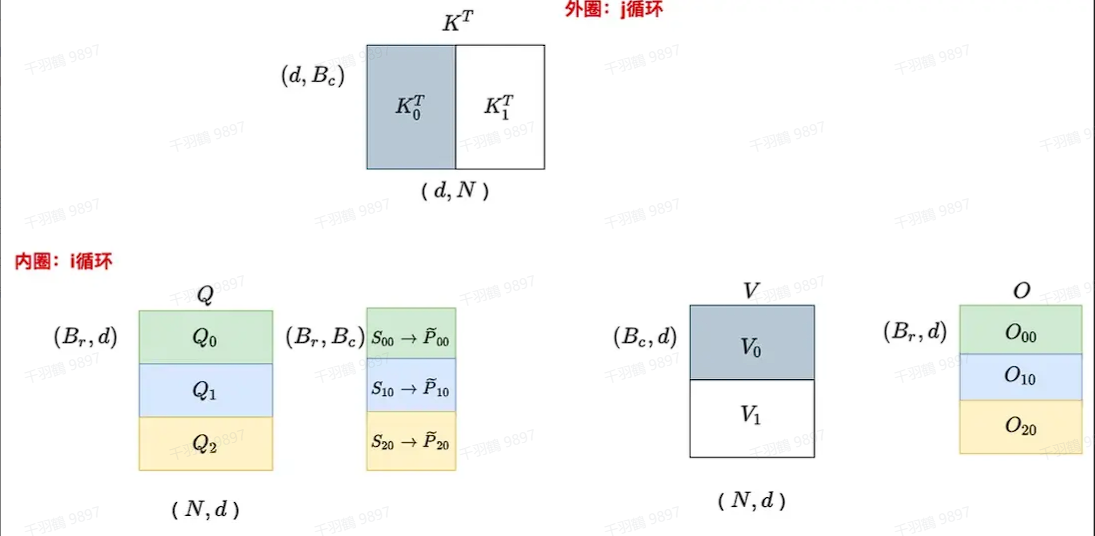
当 j=2 时

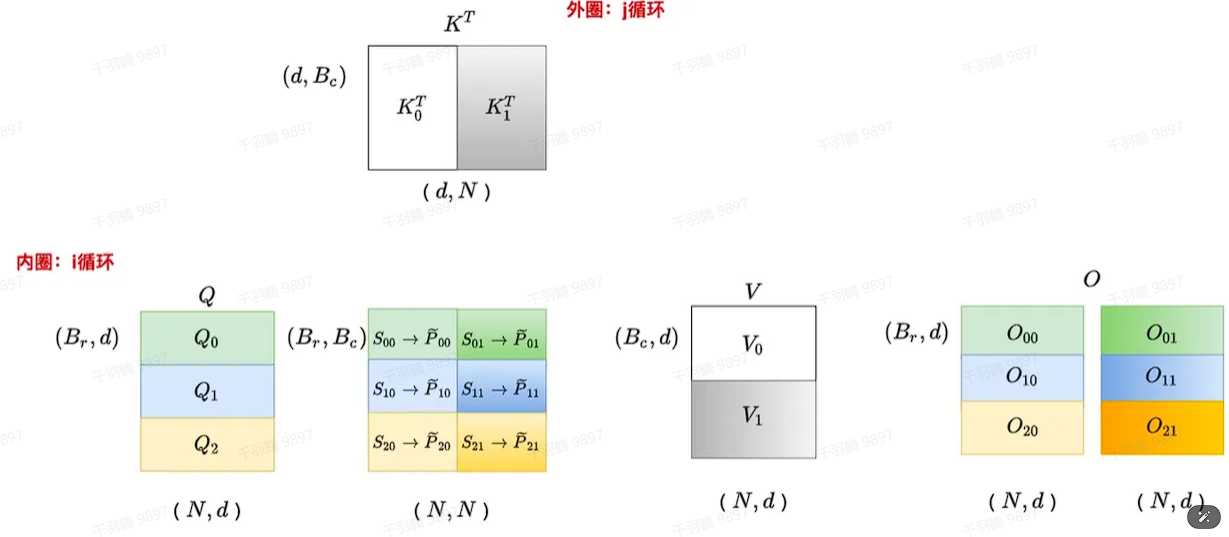
Tilling 中的 Safe Softmax

探讨 Tilling 中的 Safe Softmax 的概念及其计算方法。我们假设标准场景下，矩阵某一行的向量为

x = [x_{1}, x_{2}, \dots, x_{d}]

因为分块的原因，它被我们切成了两部分

x = [x^{(1)}, x^{(2)}]

我们定义：

在分块计算的过程中，我们将输出定义为 $O$ 。我们需要确保分块计算中的结果与标准场景下的结果完全一致。然而，由于 memory-bound 的问题，我们只保留 $m$ , $l$ , $O$ 而不存各块 $S$ , $P$ 。因此，当我们遍历到最后一块时，虽然有了全局的 rowmax 和 rowsum，但没有 $S$ , $P$ ，我们根本无法算出最终的 $O_{i}$ 。

思路转变：

为了解决这个问题，我们需要换个思路。即使我们没有每块的 $S$ , $P$ ，我们仍然可以通过不断使用当前最新的 rowmax 和 rowsum 来更新 $O_{i}$ ，直到遍历完最后一块。这时的 $O_{i}$ 就和标准场景下的结果完全一致了。我们希望构造形如下面这样的更新等式：

O_{i} = O_{i} + 当 前 最 新 结 果

更新公式：

对于每一块，我们可以通过以下公式进行更新：

O_{i}^{(j + 1)} = P_{i, : j + 1} V_{: j + 1} = softmax (S_{i, : j + 1}) V_{: j + 1}

其中，

= diag (l^{(j + 1)})^{- 1} [\exp ([S_{i, : j}, S_{i}^{(j + 1)}] - m^{(j + 1)})] [V_{: j}, V_{j + 1}]

进一步简化为：

= diag (l^{(j + 1)})^{- 1} [\exp (S_{i, : j} - m^{(j + 1)}) V_{: j} + \exp (S_{i}^{(j + 1)} - m^{(j + 1)}) V_{j + 1}]

最终我们得到：

= diag (l^{(j + 1)})^{- 1} [e^{- m^{(j + 1)}} \exp (S_{i, j}) V_{: j} + e^{- m^{(j + 1)}} \exp (S_{i}^{(j + 1)}) V_{j + 1}]

经过多次迭代更新后，我们可以表示为：

= diag (l^{(j + 1)})^{- 1} [diag (l^{(j)}) e^{m^{(j)} - m^{(j + 1)}} diag (l^{(j)})^{- 1} \exp (S_{i, : j} - m^{(j)}) V_{: j} + e^{- m^{(j)}}

最终，我们得到完整的更新公式：

= diag (l^{(j + 1)})^{- 1} [diag (l^{(j)}) e^{m^{(j)} - m^{(j + 1)}} P_{i, : j} V_{: j} + e^{- m^{(j + 1)}} \exp (S_{i}^{(j + 1)}) V_{j + 1}]

通过这样的更新方法，我们能够确保在遍历完所有块后，得到的结果与标准场景下完全一致。

Forward计算代码解析

在深度学习中，计算效率和模型性能是两个重要的考量因素。本文将详细解析一个用于前向传播（Forward Pass）的计算代码，帮助读者理解其内在逻辑和操作步骤。

import torch

NEG_INF = -1e10  # -infinity
EPSILON = 1e-10
Q_LEN = 6
K_LEN = 6
Q_BLOCK_SIZE = 3
KV_BLOCK_SIZE = 3
P_DROP = 0.2

Tr = Q_LEN // Q_BLOCK_SIZE
Tc = K_LEN // KV_BLOCK_SIZE

Q = torch.randn(1, 1, Q_LEN, 4, requires_grad=True).to(device='cpu')
K = torch.randn(1, 1, K_LEN, 4, requires_grad=True).to(device='cpu')
V = torch.randn(1, 1, K_LEN, 4, requires_grad=True).to(device='cpu')

O = torch.zeros_like(Q, requires_grad=True)
l = torch.zeros(Q.shape[:-1])[..., None]
m = torch.ones(Q.shape[:-1])[..., None] * NEG_INF

# step 4
Q_BLOCKS = torch.split(Q, Q_BLOCK_SIZE, dim=2)
K_BLOCKS = torch.split(K, KV_BLOCK_SIZE, dim=2)
V_BLOCKS = torch.split(V, KV_BLOCK_SIZE, dim=2)

# step 5
O_BLOCKS = list(torch.split(O, Q_BLOCK_SIZE, dim=2))
l_BLOCKS = list(torch.split(l, Q_BLOCK_SIZE, dim=2))
m_BLOCKS = list(torch.split(m, Q_BLOCK_SIZE, dim=2))

# step 6
for j in range(Tc):
    # step 7
    Kj = K_BLOCKS[j]
    Vj = V_BLOCKS[j]
    # step 8
    for i in range(Tr):
        # step 9
        Qi = Q_BLOCKS[i]
        Oi = O_BLOCKS[i]
        li = l_BLOCKS[i]
        mi = m_BLOCKS[i]
        # step 10
        S_ij = torch.einsum('... i d, ... j d -> ... i j', Qi, Kj)
        # step 11
        mask = S_ij.ge(0.5)
        S_ij = torch.masked_fill(S_ij, mask, value=0)
        # step 12
        m_block_ij, _ = torch.max(S_ij, dim=-1, keepdims=True)
        P_ij = torch.exp(S_ij - m_block_ij)

l = torch.cat(l_BLOCKS, dim=2)
m = torch.cat(m_BLOCKS, dim=2)

数据块的拆分

首先，我们需要将输入的数据张量 $O$ 、 $l$ 和 $m$ 按照 $Q_B L O C K_S I Z E$ 进行拆分，以便后续的操作。

O_BLOCKS = list(torch.split(O, Q_BLOCK_SIZE, dim=2))
l_BLOCKS = list(torch.split(l, Q_BLOCK_SIZE, dim=2))
m_BLOCKS = list(torch.split(m, Q_BLOCK_SIZE, dim=2))

循环计算过程

Step 6: 外层循环

我们开始遍历 $K_B L O C K S$ ，对于每一个块 $K_{j}$ 和 $V_{j}$ ，执行后续操作。

for j in range(Tc):
    Kj = K_BLOCKS[j]
    Vj = V_BLOCKS[j]

Step 8: 内层循环

在内层循环中，我们遍历 $Q_B L O C K S$ ，对于每一个块 $Q_{i}$ ，以及相应的 $O_{i}$ 、 $l_{i}$ 、 $m_{i}$ ，进行计算。

for i in range(Tr):
    Qi = Q_BLOCKS[i]
    Oi = O_BLOCKS[i]
    li = l_BLOCKS[i]
    mi = m_BLOCKS[i]

Step 10: 相似度计算

通过爱因斯坦求和约定计算相似度矩阵 $S_{i j}$ ：

S_{i j} = torch.einsum (^{'} . . . i d, . . . j d - > . . . i j^{'}, Q i, K j)

Step 11: 掩码处理

将 $S_{i j}$ 中大于等于0.5的元素置为0：

mask = S_ij.ge(0.5)
S_ij = torch.masked_fill(S_ij, mask, value=0)

Step 12: 权重计算

通过最大值归一化和指数函数计算权重矩阵 $P_{i j}$ 及其相关量：

m_b l o c k_i j,_= torch.max (S_{i j}, dim = - 1, keepdims = T r u e)

P_{i j} = torch.exp (S_{i j} - m_b l o c k_i j)

l_b l o c k_i j = torch.sum (P_{i j}, dim = - 1, keepdims = T r u e) + ϵ

P_i j_V j = torch.einsum (^{'} . . . i j, . . . j d - > . . . i d^{'}, P_{i j}, V j)

Step 13: 更新最大值和权重

更新 $m_{i}$ 和 $l_{i}$ ：

m_{i}_new = torch.maximum (m_b l o c k_i j, m_{i})

l_{i}_new = torch.exp (m_{i} - m_{i}_new) \times l_{i} + torch.exp (m_b l o c k_i j - m_{i}_new) \times l_b l o c k_i j

Step 14: Dropout操作

对 $P_{i j} V_{j}$ 应用Dropout：

m = torch.nn.Dropout(p=P_DROP)
P_ij_Vj = m(P_ij_Vj)

Step 15: 更新输出块

更新输出块 $O_{i}$ ：

O_B L O C K S [i] = \frac{l_{i}}{l_{i}_new} \times torch.exp (m_{i} - m_{i}_new) \times O_{i} + \frac{torch.exp (m_b l o c k_i j - m_{i}_new)}{l_{i}_new} \times P_{i j} V_{j}

并打印调试信息：

print(f'-----------Attention : Q {i} xK {j} ---------')
print(O_BLOCKS[i].shape)
print(O_BLOCKS[0])
print(O_BLOCKS[1])
print('\n')

Step 16: 更新块信息

将更新后的 $l_{i}$ 和 $m_{i}$ 保存回对应的块中：

l_BLOCKS[i] = li_new
m_BLOCKS[i] = mi_new

拼接结果

最后，将所有块拼接回完整的张量：

O = torch.cat(O_BLOCKS, dim=2)
l = torch.cat(l_BLOCKS, dim=2)
m = torch.cat(m_BLOCKS, dim=2)

计算量和显存

FlashAttention 计算流程

计算量

在算法第9行，我们有

S_{i j} = Q_{i} K_{j}^{T}

其中

Q_{i} \in R^{B_{r} \times d}, K_{j}^{T} \in R^{d \times B_{c}}

根据前置知识，求

S_{i j}

的计算量为

O (B_{r} B_{c} d)

在算法第12行，我们有

P_{i j} V_{j}

其中

P_{i j} \in R^{B_{r} \times B_{c}}, V_{j} \in R^{B_{c} \times d}

则这里的计算量同样为

O (B_{r} B_{c} d)

接下来我们看一共计算了多少次(1)和(2)，也就是执行了多少次内循环：

综合以上三点，flash attention的forward计算量为：

O (B_{c} B_{r} N^{2} B_{r} B_{c} d) = O (N^{2} d)

同理大家可以自行推一下backward中的计算量，在论文里给出的结论是

O (N^{2})

， $d$ 远小于 $N$ ，因此 $d$ 也可以略去不表达。

显存

和标准attention相比，如果不考虑 $O$ 的话，Flash Attention只需要存储 $m, l$ ，其显存需求为

O (N)

。而标准attention需要存储 $S, P$ ，其显存需求为

O (N^{2})

。可以发现相比于标准attention，flash attention明显降低了对显存的需求。

IO复杂度

我们来看伪代码的第六行，在每个外循环中，我们都会加载 $K, V$ 的block。所有外循环结束后，相当于我们加载了完整的

K, V \in R^{N \times d}

因此这里的IO复杂度为：

O (N d)

再看伪代码第8行，在每个内循环中，我们都加载了部分 $Q, O, m, l$ block，由于 $m, l$ 本身比较小(IO复杂度是

O (N)

)，因此我们暂时忽略它们，只考虑 $Q, O$ (原论文也是这么分析的)。固定某个外循环，所有内循环结束后，我们相当于完整遍历了

Q, O \in R^{N \times d}

。同时我们会经历 $T_{c}$ 次外循环。因此这里最终的IO复杂度为：

O (T_{c} N d)

将 $O, m, l$ 写回HBM，这里近似后IO复杂度为：

O (N d)

。不过在原论文的分析中并没有考虑写回的复杂度，不过省略一些常数项不会影响我们最终的分析。

所以，总体来说flash attention的IO复杂度为：

O (T_{c} N d) = O (B_{c} N N d) = O (M 4 N d N d) = O (M N^{2} d^{2})

。论文中提过，一般 $d$ 的取值在64～128， $M$ 的取值在100KB左右，因此有

\frac{M}{d^{2}} ≪ 1

。因此可以看出，Flash attention的IO复杂度是要显著小于标准attention的IO复杂度的。